Emin's Notes

Recent Notes

Improving Performance With SIMD intrinsics

Aug 03, 202410 min read

Modern CPUs increasingly rely on parallelism to achieve peak performance. The most well-known form is task parallelism, which is supported at the hardware level by multiple cores, hyperthreading and dedicated instructions supporting multitasking operating systems. Less known is the parallelism known as instruction level parallelism: the capability of a CPU to execute multiple instructions simultaneously, i.e., in the same cycle(s), in a single thread. Older CPUs such as the original Pentium used this to execute instructions utilizing two pipelines, concurrently with high-latency floating point operations. Typically, this happens transparent to the programmer. Recent CPUs use a radically different form of instruction level parallelism. These CPUs deploy a versatile set of vector operations: instructions that operate on 4 or 8 inputs1 , yielding 4 or 8 results, often in a single cycle. This is known as SIMD: Single Instruction, Multiple Data. To leverage this compute potential, we can no longer rely on the compiler. Algorithms that exhibit extensive data parallelism benefit most from explicit SIMD programming, with potential performance gains of 4x - 8x and more.

Outside of niche areas like high-performance computing, game development, or compiler development, even very experienced C and C++ programmers are largely unfamiliar with SIMD intrinsics.

Concepts

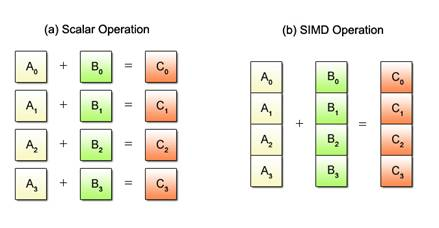
Registers are used by a CPU to store data for operations. A typical register holds 32 or 64 bits. Some of these registers can be split in to 16bit parts or even single bytes.

Vector registers store 4 (SSE) or 8 (AVX) scalars. This means that the C# or C++ vector remains a vector at the assembler level: rather than storing 4 separate values in 4 registers, we store 4 values in a single vector register. And rather than operating on a, b, c and d separately, we use a single SIMD instruction to perform addition (for example) to all 4 values.

If you’re a C++ programmer, you’re probably familiar with the basic types like char, short, int, and float. Each of these has a different size: A char has 8 bits, a short has 16, an int has 32, and a float has 32. Because bits are just bits, the only difference between a float and an int is in the interpretation. This enables us to do some nasty things:

int a;
float& b = (float&)a;

This creates one integer and a float reference to a. Because variables a and b now share the same memory location, changing one changes the other. An alternative way to achieve this is using a union:

union { int a; float b; };

Again, a and b reside in the same memory location. Here’s another example:

union { unsigned int a4; unsigned char a[4]; };

This time, a small array of four chars overlaps the 32-bit integer value a4. We can now access the individual bytes in a4 via array a[4]. Note that a4 now basically has four 1-byte ‘lanes’, which is somewhat similar to what we get with SIMD. We could even use a4 as 32 1-bit values, which is an efficient way to store 32 boolean values.

An SSE register is 128 bits in size and is labeled __m128 if it stores four floats or __m128i if it stores ints. For simplicity, we will refer to __m128 as ‘quadfloat’ and __m128i as ‘quadint’. __m256 (‘octfloat’) and __m256i (‘octint’) are the AVX versions. To use the SIMD types, we need to include the following headers:

#include "nmmintrin.h" // for SSE4.2
#include "immintrin.h" // for AVX

A __m128 variable contains four floats, so we can use the union trick again:

union { __m128 a4; float a[4]; };

Now we can conveniently access the individual floats in the __m128 vector. We can also create the quadfloat directly:

__m128 a4 = _mm_set_ps( 4.0f, 4.1f, 4.2f, 4.3f );
__m128 b4 = _mm_set_ps( 1.0f, 1.0f, 1.0f, 1.0f );

To add them together, we use __mm_add_ps:

__m128 sum4 = _mm_add_ps( a4, b4 );

The __mm_set_ps and _mm_add_ps keywords are called intrinsics. SSE and AVX intrinsics all compile to a single assembler instruction; using these means that we are essentially writing assembler code directly in our program.

Examples

Basic Addition

#include <immintrin.h>
#include <stdio.h>
 
int main(int argc, char** argv) {
    const int N = 16;
    float a[N], b[N], c[N];
    // Initialize arrays
    for (int i = 0; i < N; i++) {
        a[i] = (float)i;
        b[i] = 2.0f;
    }
    // Perform element-wise addition using vector instructions
    __m256 a_vec, b_vec;
    for (int i = 0; i < N; i += 8) {
        a_vec = _mm256_load_ps(&a[i]);
        b_vec = _mm256_load_ps(&b[i]);
        _mm256_store_ps(&c[i], _mm256_add_ps(a_vec, b_vec));
    }
    // Print the result
    for (int i = 0; i < N; i++) {
        printf("%f + %f = %f\n", a[i], b[i], c[i]);
    }
    return 0;
}

This code performs element-wise addition of two arrays a and b, and stores the result in c. The addition is performed using vector instructions from the AVX instruction set, which allows us to operate on 8 elements at a time. This can result in significant performance improvements compared to a scalar implementation, especially on systems with support for hardware acceleration of vector instructions.

Dot Product

One accumulator, no FMA

float dotProduct(const float* p1, const float* p2, size_t count) {
    if (count % 8 != 0)
        return 0.0f;
    __m256 acc = _mm256_setzero_ps();
    // p1End points to the end of the array, so that we don't process past the end.
    const float* const p1End = p1 + count;
    for (; p1 < p1End; p1 += 8, p2 += 8) {
        // Load 2 vectors, 8 floats / each
        const __m256 a = _mm256_loadu_ps(p1);
        const __m256 b = _mm256_loadu_ps(p2);
        // vdpps AVX instruction does not compute dot product of 8-wide vectors.
        // Instead, that instruction computes 2 independent dot products of
        // 4-wide vectors.
        const __m256 dp = _mm256_dp_ps(a, b, 0xFF);
        acc = _mm256_add_ps(acc, dp);
    }
    // Add the 2 results into a single float.
    const __m128 low = _mm256_castps256_ps128(acc);     //< Compiles into no instructions. The low half of a YMM register
                                                        // is directly accessible as an XMM register with the same
                                                        // number.
    const __m128 high = _mm256_extractf128_ps(acc, 1);  //< This one however does need to move data, from high half of a
                                                        // register into low half. vextractf128 instruction does that.
    // Add the first element of two __m128 vectors (low and high)
    const __m128 result = _mm_add_ss(low, high);
    // By the way, the intrinsic below compiles into no instructions.  
	// When a function is returning a float, modern compilers pass the return value in the lowest lane of xmm0 vector register.
    return _mm_cvtss_f32(result);
}

This function calculates dot product without using FMA(Fused Multipy and Add) instructions and using a single accumulator.

Why multiple accumulators?

Data dependencies is the main thing I’d like to illustrate with this example.

From a computer scientist point of view, dot product is a form of reduction. The algorithm needs to process large input vectors, and compute just a single value. When the computations are fast (like in this case, multiplying floats from sequential blocks of memory is very fast), the throughput is often limited by latency of the reduce operation.

Let’s compare code of two specific versions, AvxVerticalFma and AvxVerticalFma2. The former has the following main loop:

for (; p1 < p1End; p1 += 8, p2 += 8) {  
    const __m256 a = __mm256_loadu_ps_(p1);  
    const __m256 b = __mm256_loadu_ps_(p2);  
    acc = _mm256_fmadd_ps(a, b, acc);  // Update the only accumulator  
}

AvxVerticalFma2 version runs following code:

for (; p1 < p1End; p1 += 16, p2 += 16) {  
    __m256 a = __mm256_loadu_ps_(p1);  
    __m256 b = __mm256_loadu_ps_(p2);  
    dot0 = __mm256_fmadd_ps_(a, b, dot0);  // Update the first accumulator  
    a = __mm256_loadu_ps_(p1 + 8);  
    b = __mm256_loadu_ps_(p2 + 8);  
    dot1 = __mm256_fmadd_ps_(a, b, dot1);  // Update the second accumulator  
}

_mm256_fmadd_ps intrinsic computes (a*b)+c for arrays of eight float values, that instruction is part of FMA3 instruction set. The reason why AvxVerticalFma2 version is almost 2x faster—deeper pipelining hiding the latency.

When the processor submits an instruction, it needs values of the arguments. If some of them are not yet available, the processor waits for them to arrive. The tables on https://www.agner.org/ say on AMD Ryzen the latency of that FMA instruction is five cycles. This means once the processor started to execute that instruction, the result of the computation will only arrive five CPU cycles later. When the loop is running a single FMA instruction which needs the result computed by the previous loop iteration, that loop can only run one iteration in five CPU cycles.

With two accumulators that limit is the same, five cycles. However, the loop body now contains two FMA instructions that don’t depend on each other. These two instructions run in parallel, and the code delivers twice the throughput on the desktop.

Optimizing and Debugging SIMD Code, Hints

In the previous sections, we discussed how to vectorize code and handle conditional code. In this section, we will explore some common opportunities for improving the efficiency of SIMD code.

Instruction count is an important factor in program size and speed. As a general rule, shorter source code leads to smaller and faster programs. Advanced instructions, such as _mm_blendv_ps, can often replace a sequence of simpler instructions. It is useful to become familiar with the available instructions.

Floating point support in SSE and AVX is generally better than integer support. In some cases, converting temporary integers to floats can result in more efficient code, even if conversion back to integers is necessary. Floating point arithmetic is often simpler than integer intrinsics, some of which can be quite obscure, such as _mm_mullo_epi32.

Frequent use of _mm_set_ps to create constants in vectorized code can be costly since it takes four operands. To avoid this, consider caching the quadfloat outside loops so it can be used many times inside the loop without penalty. If scalars need to be expanded to quadfloats, consider caching the expanded version in the class.

Gather operations, which rely on scattered memory locations, can cause issues related to _mm_set_ps. For faster data retrieval from memory to quadfloat, it is best to have the data already stored as a quadfloat in 16 consecutive bytes of memory.

Data alignment is crucial when working with quadfloats since they must always be stored at a multiple of 16 in memory. In C++, variables created on the stack will automatically follow this rule, but variables allocated using new may not be aligned, leading to unexpected crashes. Checking whether the data being processed is properly aligned can help diagnose crashes.

Support for SIMD is well-integrated in the Jetbrains Clion. It allows for effortless inspection of individual values in SIMD variables.

When using AVX/AVX2 instructions, ensure that the target hardware is compatible. If the code is not compatible, provide an alternative implementation for older hardware. Failing to do so may cause unexpected crashes or performance issues.

Focus vectorization efforts on bottlenecks only. In real-world situations, it is best to focus vectorization efforts on bottlenecks only, such as a large loop that updates variables.

Evade fancy SIMD libraries Vectorization is hard, and it feels unnatural to write _mm_mul_ps(a,b) when you meant to write a * b. Resist the urge to write your own operators; get used to the raw intrinsics. Anything more complex is bound to hide inefficiencies or even introduce them. Besides, some SIMD in your code makes it look like wizardry (which it is, in fact). If you must use something convenient, consider Agner Fog’s vector library: http://www.agner.org/optimize/#vectorclass . Also read the rest of his site, the man is a guru of software optimization.

See Also

Graph View

Backlinks